그래프의 기본 구조
예전 포스팅 (https://emperor-one-data-study.tistory.com/45) 에서도 언급했듯이 그래프는 node와 edge (간선)로 구성되어 있다. 프로그램에서 그래프를 나타내는 방식으로는 인접 리스트와 인접 행렬이 있는데 두 가지 표현 방식을 파이썬 코드로 알아보았다.
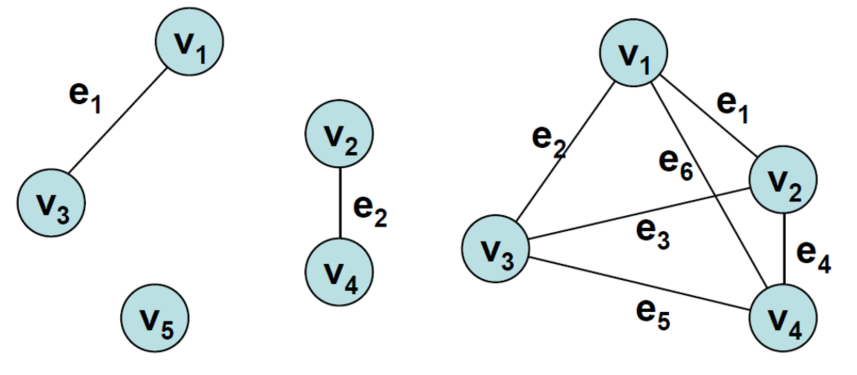
인접 행렬 (adjacency matrix)
- 2차원 배열에 각 노드가 연결된 형식
- 파이썬에서는 2차원 리스트로 구현할 수 있음
- 연결되어 있지 않은 노드끼리는 무한의 비용이라고 작성함 (실제 코드에서는 논리적으로 정답이 될 수 없는 큰 값 중에서 9999999999 등의 값으로 초기화하는 경우가 많음)
| 0 | 1 | 2 | |
| 0 | 0 | 7 | 5 |
| 1 | 7 | 0 | 무한 |
| 2 | 5 | 무한 | 0 |
0,1,2를 노드로 하는 그래프에서 각 연결 관계를 나타낸 표이다. 1,2는 연결되어 있지 않아 무한으로 표현하였다.
INF = 9999999999999 #무한 비용 선언
graph = [
[0,7,5],
[7,0, INF],
[5, INF, 0]
]
print(graph)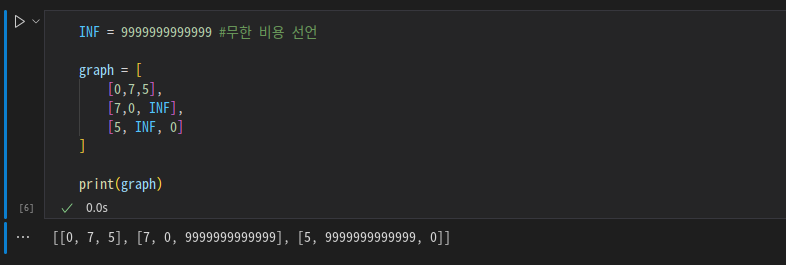
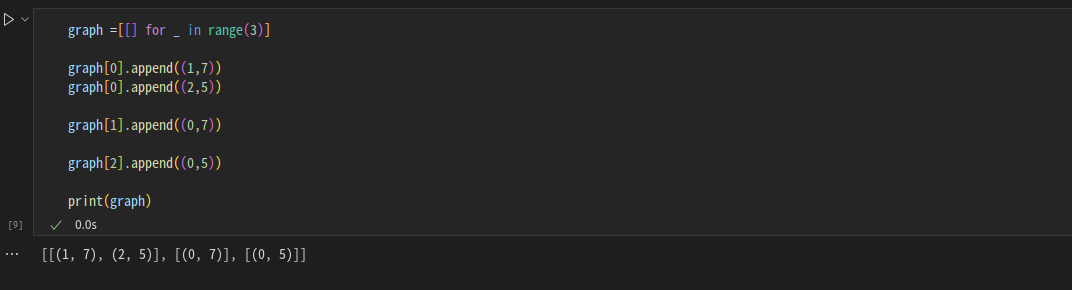
인접 리스트 (adjacency list)
- 모든 노드에 연결된 노드에 대한 정보를 차례대로 연결하여 저장함
- 모든 결과를 나타냈던 인접행렬과는 다른 방식
- append를 통해 다타낼 수 있음
- 연결된 정보만을 나타내기 때문에 메모리를 효율적으로 사용할 수 있음
DFS, BFS 함수를 정의하고 문제를 풀면 더 쉽게 구현할 수 있다 !
DFS (Depth- First Search)
- 깊이 우선 탐색, 최대한 멀리있는 노드를 우선으로 탐색
- 그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘 , 스택 자료구조 이용, 재귀함수 이용해서 더 간단하게 구현 가능
- 동작 과정
1. 탐색 시작 노드를 스택에 삽입하고 방문 처리
2. 스택의 최상단 노드에 방문하지 않은 인접 노드가 있으면 그 인접 노드를 스택에 넣고 방문 처리, 방문하지 않은 인접 노드가 없으면 스택에서 최상단 노드 꺼냄
3. 2번의 과정을 더 이상 수행할 수 없을 때까지 반복
- 방문처리란?: 스택에 한번 삽입되어 처리된 노드가 다시 삽입하지 않게 체크하는 것, 각 노드를 한번만 처리할 수 있도록 함
BFS (Breadth First Search)
- 너비 우선 탐색
- 가까운 노드부터 탐색
- 큐 자료 구조 활용 (선입선출), deque 라이브러리 활용하자
- 동작 과정
1. 탐색 시작 노드를 큐에 삽입하고 방문 처리
2. 큐에서 노드를 꺼내 해당 노드의 인접 노드 중에서 방문하지 않은 노드를 모두 큐에 삽입하고 방문처리
3. 2번 과정 더 이상 수행할 수 없을 때까지 반복
- 보통 DFS보다 BFS이 조금 더 빠르게 동작한다!
아웅 복잡하긴한데 ,, 역시 문제로 푸는게 훨씬 더 와닿긴하다.
백준 문제

from collections import deque
N, M, V = map(int, input().split())
graph = [[0] * (N + 1) for _ in range(N + 1)]
for _ in range(M):
m1, m2 = map(int, input().split())
graph[m1][m2] = graph[m2][m1] = 1
def bfs(start_v):
discoverd = [start_v]
queue = deque()
queue.append(start_v)
while queue:
v = queue.popleft()
print(v, end=' ')
for w in range(len(graph[start_v])):
if graph[v][w] == 1 and (w not in discoverd):
discoverd.append(w)
queue.append(w)
def dfs(start_v, discoverd=[]):
discoverd.append(start_v)
print(start_v, end=' ')
for w in range(len(graph[start_v])):
if graph[start_v][w] == 1 and (w not in discoverd):
dfs(w, discoverd)
dfs(V)
print()
bfs(V)책에 있는 구현 방식을 따라가며 따라해 봤다 !
'Algorithm' 카테고리의 다른 글
| 2진수, 3진수, k진수 변환하는 법 | 파이썬 k진수 변환 | 소수찾기 | 프로그래머스 k진수에서 소수찾기 파이썬 (0) | 2024.02.15 |
|---|---|
| [코딩테스트/ Python] 시간을 단축시켜주는 정규 표현식/프로그래머스 신규 아이디 추천 (1) | 2023.06.11 |
| [코딩테스트/Python] 꼭 필요한 자료구조 기초: 재귀함수 (0) | 2023.05.08 |
| [코딩테스트 /Python] 프로그래머스 기능 개발 (0) | 2023.05.04 |
| [코딩테스트/Python] 프로그래머스 두 큐 합 같게 만들기 (0) | 2023.05.01 |
그래프의 기본 구조
예전 포스팅 (https://emperor-one-data-study.tistory.com/45) 에서도 언급했듯이 그래프는 node와 edge (간선)로 구성되어 있다. 프로그램에서 그래프를 나타내는 방식으로는 인접 리스트와 인접 행렬이 있는데 두 가지 표현 방식을 파이썬 코드로 알아보았다.

인접 행렬 (adjacency matrix)
- 2차원 배열에 각 노드가 연결된 형식
- 파이썬에서는 2차원 리스트로 구현할 수 있음
- 연결되어 있지 않은 노드끼리는 무한의 비용이라고 작성함 (실제 코드에서는 논리적으로 정답이 될 수 없는 큰 값 중에서 9999999999 등의 값으로 초기화하는 경우가 많음)
| 0 | 1 | 2 | |
| 0 | 0 | 7 | 5 |
| 1 | 7 | 0 | 무한 |
| 2 | 5 | 무한 | 0 |
0,1,2를 노드로 하는 그래프에서 각 연결 관계를 나타낸 표이다. 1,2는 연결되어 있지 않아 무한으로 표현하였다.
INF = 9999999999999 #무한 비용 선언
graph = [
[0,7,5],
[7,0, INF],
[5, INF, 0]
]
print(graph)
인접 리스트 (adjacency list)
- 모든 노드에 연결된 노드에 대한 정보를 차례대로 연결하여 저장함
- 모든 결과를 나타냈던 인접행렬과는 다른 방식
- append를 통해 다타낼 수 있음
- 연결된 정보만을 나타내기 때문에 메모리를 효율적으로 사용할 수 있음

DFS, BFS 함수를 정의하고 문제를 풀면 더 쉽게 구현할 수 있다 !
DFS (Depth- First Search)
- 깊이 우선 탐색, 최대한 멀리있는 노드를 우선으로 탐색
- 그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘 , 스택 자료구조 이용, 재귀함수 이용해서 더 간단하게 구현 가능
- 동작 과정
1. 탐색 시작 노드를 스택에 삽입하고 방문 처리
2. 스택의 최상단 노드에 방문하지 않은 인접 노드가 있으면 그 인접 노드를 스택에 넣고 방문 처리, 방문하지 않은 인접 노드가 없으면 스택에서 최상단 노드 꺼냄
3. 2번의 과정을 더 이상 수행할 수 없을 때까지 반복
- 방문처리란?: 스택에 한번 삽입되어 처리된 노드가 다시 삽입하지 않게 체크하는 것, 각 노드를 한번만 처리할 수 있도록 함
BFS (Breadth First Search)
- 너비 우선 탐색
- 가까운 노드부터 탐색
- 큐 자료 구조 활용 (선입선출), deque 라이브러리 활용하자
- 동작 과정
1. 탐색 시작 노드를 큐에 삽입하고 방문 처리
2. 큐에서 노드를 꺼내 해당 노드의 인접 노드 중에서 방문하지 않은 노드를 모두 큐에 삽입하고 방문처리
3. 2번 과정 더 이상 수행할 수 없을 때까지 반복
- 보통 DFS보다 BFS이 조금 더 빠르게 동작한다!
아웅 복잡하긴한데 ,, 역시 문제로 푸는게 훨씬 더 와닿긴하다.
백준 문제

from collections import deque
N, M, V = map(int, input().split())
graph = [[0] * (N + 1) for _ in range(N + 1)]
for _ in range(M):
m1, m2 = map(int, input().split())
graph[m1][m2] = graph[m2][m1] = 1
def bfs(start_v):
discoverd = [start_v]
queue = deque()
queue.append(start_v)
while queue:
v = queue.popleft()
print(v, end=' ')
for w in range(len(graph[start_v])):
if graph[v][w] == 1 and (w not in discoverd):
discoverd.append(w)
queue.append(w)
def dfs(start_v, discoverd=[]):
discoverd.append(start_v)
print(start_v, end=' ')
for w in range(len(graph[start_v])):
if graph[start_v][w] == 1 and (w not in discoverd):
dfs(w, discoverd)
dfs(V)
print()
bfs(V)책에 있는 구현 방식을 따라가며 따라해 봤다 !
'Algorithm' 카테고리의 다른 글
| 2진수, 3진수, k진수 변환하는 법 | 파이썬 k진수 변환 | 소수찾기 | 프로그래머스 k진수에서 소수찾기 파이썬 (0) | 2024.02.15 |
|---|---|
| [코딩테스트/ Python] 시간을 단축시켜주는 정규 표현식/프로그래머스 신규 아이디 추천 (1) | 2023.06.11 |
| [코딩테스트/Python] 꼭 필요한 자료구조 기초: 재귀함수 (0) | 2023.05.08 |
| [코딩테스트 /Python] 프로그래머스 기능 개발 (0) | 2023.05.04 |
| [코딩테스트/Python] 프로그래머스 두 큐 합 같게 만들기 (0) | 2023.05.01 |
