Recap & step function을 활용한 classification model
- linear classification task를 수행하기 위해서는 $(x_1, x_2)$라는 feature를 활용하여 decision boundary를 생성하였음.
- 하지만 선형의 decision boundary로 데이터를 분류할 수 없는 경우가 있다.

- 위와 같은 경우에는 선형으로는 분류할 수 없다. 따라서 다양한 정보를 나타내기 위하여 $\phi(x)=[x_1, x_2, x_1^2, x_1x_2, x_2^2]^T$를 사용할 수 있다. 이는 $x$를 활용하여 여러 feature 생성한 것인데 1차원이 아닌 2차원 feature가 포함되어 있으므로 polynomial features하고 할 수 있다.
- 여러 정보를 반영하기 위해, linear하지 않은 데이터에 대해서도 적용할 수 있는 분류기를 만들기 위해 polynomial feature말고도 다양한 feature를 활용할 수 있음.
- 그 중 한 개념이 feature로 step function 그 자체를 feature로 활용하는 것.
- step function을 feature로 사용한다는 것이 무슨 말일까?
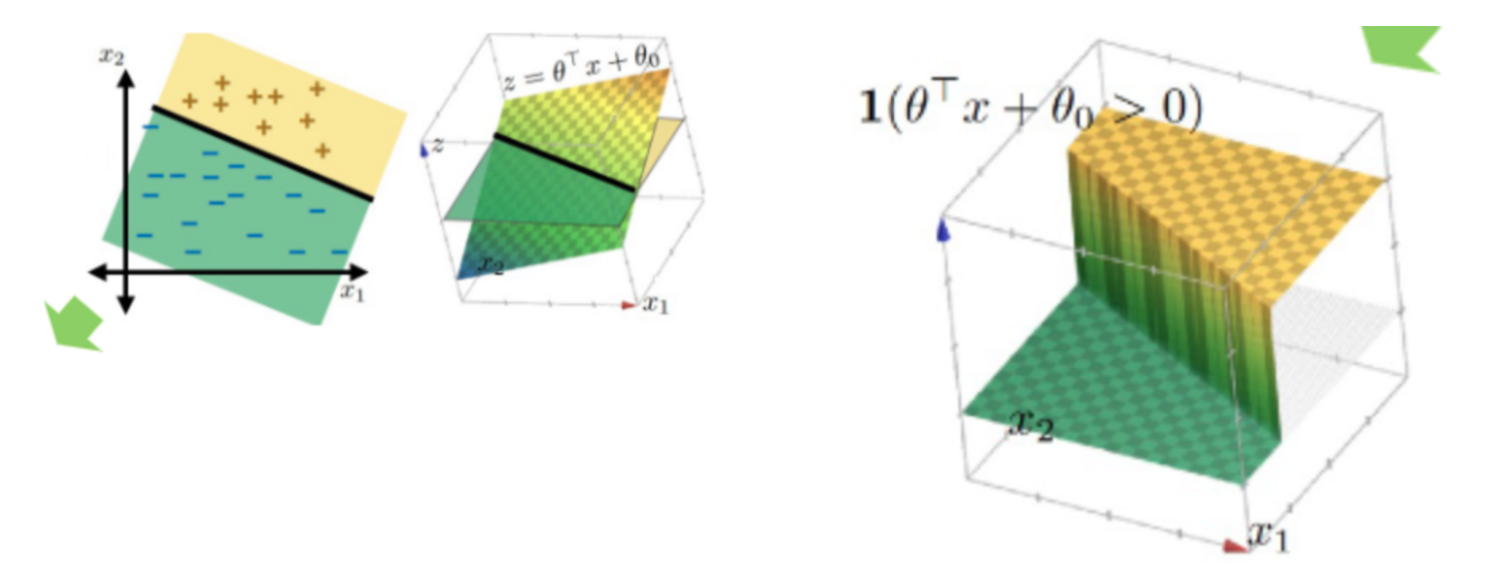
- default feature를 활용하여 분류를 진행할 때, 다음 그림과 같이 step function을 활용할 수 있었다.
- indicator 함수를 활용하여 $I(\theta^Tx+\theta_0>0)$ , $z=\theta_Tx +\theta_0$ 선형선보다 작은지 큰지에 따라 +,-로 분류할 수 있었다.
- 이 식에서는 기울기와 절편에 해당하는 $\theta , \theta_0$에 따라 line이 달라졌다. 즉, $\theta$를 학습시켰다. 하지만 이를 고정시키고 다양한 $x$를 고려해보고자 한다.
- $x$에 대한 함수 $\phi(x)$는 새로운 절편 $w^T, w_0$을 가지는 식으로 만들 수 있다. 미리 feature를 지정하지 말고 어떤 feature를 사용할지 골라보자는 것이다.
- 여기서, $\theta$는 고정으로 생각한다.

- 그림과 같이 $x$에 대한 여러 함수를 정의할 수 있고 이를 바탕으로 새로운 hyperplane을 정의할 수 있다.
- $w^T, w_0$을 학습시켜 best hyperplane을 찾을 수 있음.
Simple NN
- 해당 방법을 사용하여 Weight $w$를 학습시키는 간단한 nueral network를 구축할 수 있음
- 두 개의 layer : feature 생성 layer + classification layer
- feature 생성 layer는 hidden layer에 속한다
300x250
